Ticks search tree
Relevant and important files:
base/TickStructure.sol
libraries/TickTree.sol
TickTree
The tick tree logic is very similar to, and partially compatible with, the tick bitmap logic used in UniswapV3 - the tree uses bitmaps to store information in the nodes of the tree.
Leaves
All ticks are divided into "bundles" of 256 and packed into bitmaps. This structure is called tickTable. tickTable consists of "words" in which each bit corresponds to a tick. If a bit is 1, the tick is active. If the bit is 0, the tick is not active. Indexing of ticks in tickTable goes from right to left, i.e. tick with index 0 in a word is the lowest bit.

Within one word it is quite easy to find the next active tick after the i-th tick, if it exists. To do this, all other bits are zeroed and the getSingleSignificantBit method is used. However, if the nearest next active tick is not in the current word, the search task becomes more complicated: in the worst case, it may be necessary to search all other words in the same style, which is very expensive. For this reason, we complicate the structure of ticks by turning it into a tree.
Intermediate layer
Since one tickTable word can only store information about 256 ticks, another layer of bitmaps is added. In the intermediate layer, each word contains information about words from tickTable. Each bit in a word from the intermediate layer corresponds to a word from the leaf layer (tickTable) and is 1 if at least one bit in the corresponding word is 1 (at least one tick is active).

Thus, one word of the intermediate layer allows to find out if there is at least one active tick among 256 * 256 (65 536) ticks and to find in which word of the leaves layer it is located.
Ticks themselves can have negative indices. However, to simplify the logic, the indexing in the second layer is shifted to positive values (the tick N corresponds to the word K = floor(N / 256) + 3466 ).
However, the allowed active ticks can be much more than 65536. That's why the problem of searching remains, if the active tick is so far away that we have to search even for the words of the second level. To avoid such a search there is a third level in the tree, which is called the root.
Root
The root of the tree is also a bitmap and contains information about the words of the second (intermediate) level.
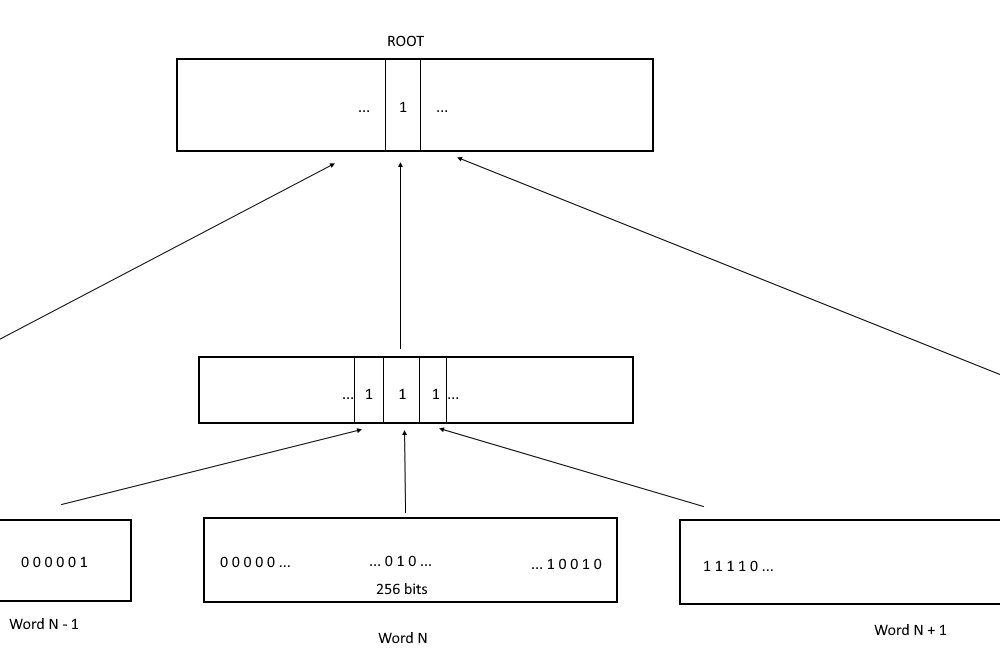
The corresponding bit at the root is 1 if the corresponding second-level word has at least one active bit.
The maximum allowed tick is 887272
The minimum allowed tick is -887272.
Thus, there can be (887272 + 887272 + 1).
Then the first level of the tree has ceil((887272 + 887272 + 1) / 256) leaves, i.e. 6932 leaves.
Then the second level needs ceil(6932 / 256) nodes, i.e. 28 nodes.
Thus, the root must store information about 28 descendants and a 32-bit value is sufficient to record it.
Worst case search
In the worst case, the current search algorithm (getNextTick method in TickTree.sol) in Algebra Integral is as follows:
Check the current leaf if it contains the next active tick
Check the current node of the intermediate layer if it has the next active leaf
Find in the root which node in the intermediate layer has an active leaf
Find in the intermediate layer node which leaf has an active tick
Find the index of the active tick in the leaf