Ticks

Relevant and important files:

• base/TickStructure.sol

Ticks

The entire price space is divided into sections using special cut-offs called ticks.

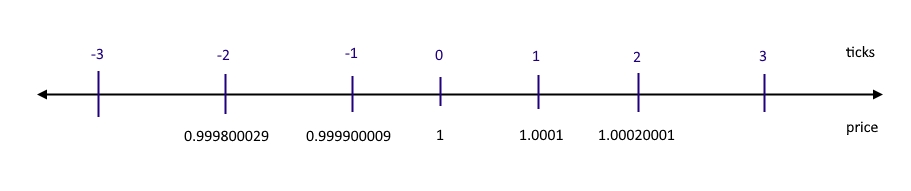
The ticks are distributed logarithmically: the tick with index i corresponds to the price:

$P(t_i) = 1.0001^i$

Inside the segment defined by two neighbouring ticks (often this segment is also called a tick), the AMM behaves like a regular CPF-AMM (like UniV2). When the price crosses a tick, the value of active liquidity may change (if the boundary of someone's position is crossed).

For this reason, when making swaps, you should be able to find the next active tick (a tick that is the boundary of a position).

Doubly linked tick list

To simplify navigation through ticks during swaps and for other purposes, Algebra Integral organises ticks as a doubly linked list: each tick stores pointers (indices) of the next and previous active ticks.

The list always contains the minimum and maximum possible ticks (as boundary values). Therefore, the list is never empty.

The pool always stores information about which ticks are currently the next and previous active ticks, so when swapping, it is easy to get information about which tick a particular iteration of the swap is up to. In each tick, the indices of the previous and next active ticks are stored in the same storage slot along with the liquidity delta, which makes it cheaper to navigate through the ticks when swapping.

However, when adding liquidity, it is necessary to have access to an arbitrary section of the doubly linked list (to insert a new tick into the list). For this purpose, Algebra Integral implements a ticks search tree.

Determination of fee increment within the range of ticks

Ticks play an important role in allocating the commission between liquidity positions. The accumulator values described in the article on liquidity and positions are used for this purpose:

$totalFeeGrowthToken0 = \sum F^x_{amount} / L_t$

$totalFeeGrowthToken1 = \sum F^y_{amount} / L_t$

Two additional values are stored in each tick that correspond to the accumulator increments "outside" the ticks: outerFeeGrowth0Token, outerFeeGrowth1Token.

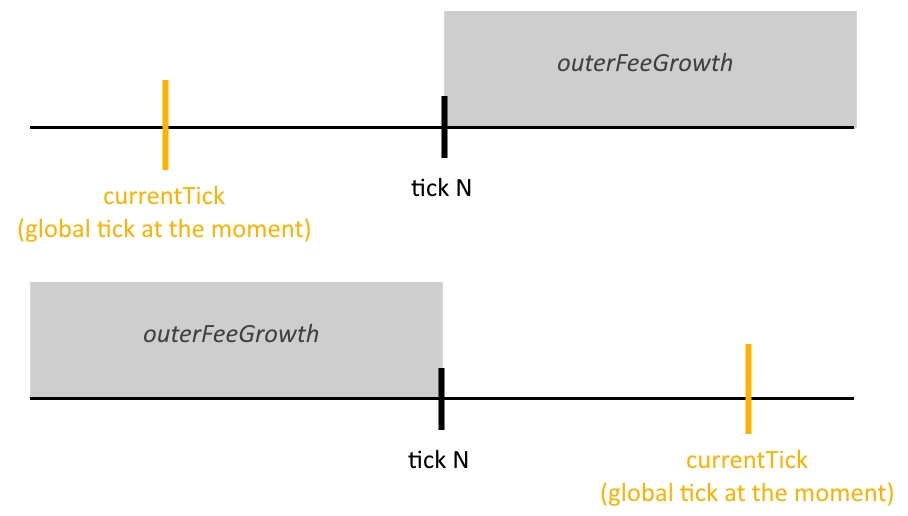
These values have a relative character and are set at the moment of tick initialisation according to the following rule: it is presumed that the entire "increment" of the commission accumulator occurred below this tick. For this reason, the values are initialised as follows:

If the tick to be initialised is less than or equal to the global tick at the moment$(tick \le currentTick)$:

$outerFeeGrowth0Token = totalFeeGrowthToken0$

$outerFeeGrowth1Token = totalFeeGrowthToken1$

On the other hand, if the tick to be initialised is above the current global tick $(tick \gt currentTick)$, then the corresponding values are initialised to zero:

$outerFeeGrowth0Token = 0$

$outerFeeGrowth1Token = 0$

Later on, at each tick crossing these values are updated according to the following rule:

$outerFeeGrowth0Token_{new} = totalFeeGrowthToken0 - outerFeeGrowth0Token_{old}$

$outerFeeGrowth1Token_{new} = totalFeeGrowthToken1 - outerFeeGrowth1Token_{old}$

This ensures that, knowing the current global tick, it is possible at any time to determine what token increment has occurred "on the other side" since the tick was initialised:

outerFeeGrowth - commission accumulator increment "on the other side" from tick N

At the same time, the pool possesses the accumulator values totalFeeGrowthToken0 and totalFeeGrowthToken1, which contain the total commission increment for the entire time of the pool's existence.

Relevant and important files:

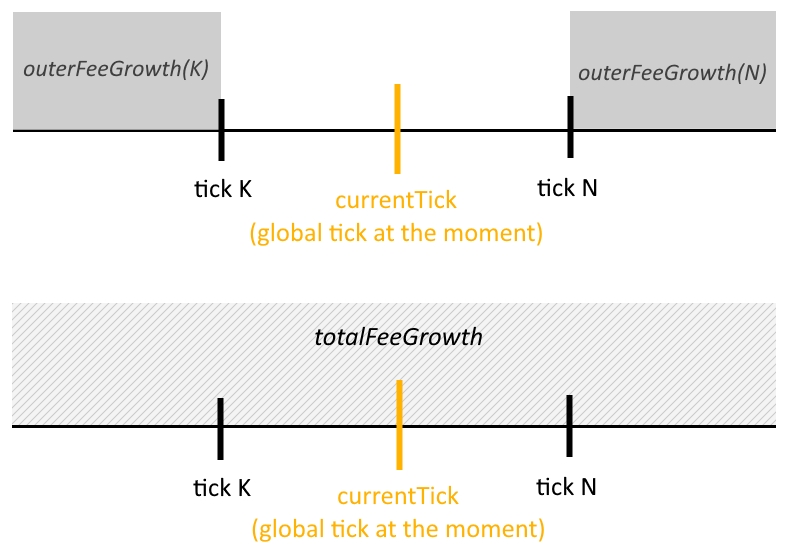
Due to these values, it is easy to calculate the value of the commission increment that occurred within a given range of ticks after their initialisation.

If $tick_K \le currentTick \lt tick_N$:

innerFeeGrowth - increment of accumulator fee / L from the moment of ticks initialisation

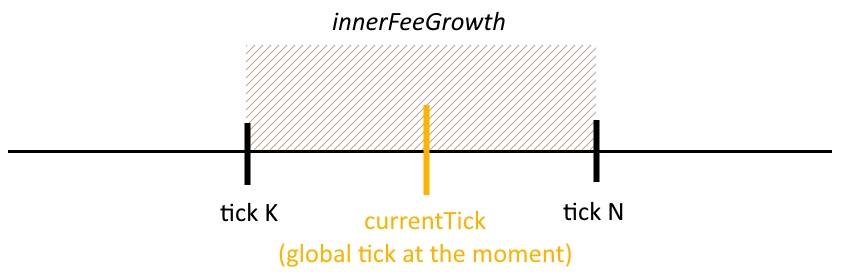
If $tick_K \lt tick_N \le currentTick$:

$innerFeeGrowth_{K, N} = outerFeeGrowth_N - outerFeeGrowth_K$

If $currentTick \lt tick_K \lt tick_N$:

$innerFeeGrowth_{K, N} = outerFeeGrowth_K - outerFeeGrowth_N$

Thus, using the above formulas for innerFeeGrowth it is possible to know the accumulator increment $\sum F^{x, y}_{amount} / L_t$ within the range specified by any two active ticks at any time. Distribution of commission among liquidity positions is performed by tracking the change of innerFeeGrowth for a liquidity position:

$\Delta fee_{position} = \Delta L_{position} * \Delta innerFeeFrowth _{position}$

Note: a similar mechanism can be used in plugins to implement time tracking within a range of ticks, distribute additional rewards, etc.